Aerodynamic Optimization
Introduction
We will now demonstrate how to optimize the aerodynamic shape of a wing. We will be combining aspects of all of the following sections: Analysis with ADflow, Optimization with pyOptSparse, and Geometric Parametrization. The optimization problem is defined as
Files
Navigate to the directory opt/aero in your tutorial folder.
Create the following empty runscript in the current directory:
aero_opt.py
Dissecting the aerodynamic optimization script
Open the file aero_opt.py in your favorite text editor.
Then copy the code from each of the following sections into this file.
Import libraries
import os
import argparse
import ast
import numpy as np
from mpi4py import MPI
from baseclasses import AeroProblem
from adflow import ADFLOW
from pygeo import DVGeometry, DVConstraints
from pyoptsparse import Optimization, OPT
from idwarp import USMesh
from multipoint import multiPointSparse
The multipoint library is the only new library to include in this script.
Adding command line arguments
# Use Python's built-in Argument parser to get commandline options
parser = argparse.ArgumentParser()
parser.add_argument("--output", type=str, default="output")
parser.add_argument("--opt", type=str, default="SLSQP", choices=["IPOPT", "SLSQP", "SNOPT"])
parser.add_argument("--gridFile", type=str, default="../../wing/meshing/volume/wing_vol_L4.cgns")
parser.add_argument("--optOptions", type=ast.literal_eval, default={}, help="additional optimizer options to be added")
args = parser.parse_args()
This is a convenience feature that allows the user to pass in command line arguments to the script. Two options are provided:
specifying the output directory
specifying the optimizer to be used
Creating processor sets
MP = multiPointSparse(MPI.COMM_WORLD)
MP.addProcessorSet("cruise", nMembers=1, memberSizes=MPI.COMM_WORLD.size)
comm, setComm, setFlags, groupFlags, ptID = MP.createCommunicators()
if not os.path.exists(args.output):
if comm.rank == 0:
os.mkdir(args.output)
The multiPointSparse class allows us to allocate sets of processors for different analyses. This can be helpful if we want to consider multiple design points, each with a different set of flow conditions. In this case, we create a processor set for cruise cases, but we only add one point.
If we want to add more points, we can increase the quantity nMembers.
We can choose the number of processors per point with the argument memberSizes.
We can add another processor set with another call to addProcessorSet.
The call createCommunicators returns information about the current processor’s set.
ADflow set-up
aeroOptions = {
# I/O Parameters
"gridFile": args.gridFile,
"outputDirectory": args.output,
"monitorvariables": ["resrho", "cl", "cd"],
"writeTecplotSurfaceSolution": True,
# Physics Parameters
"equationType": "RANS",
# Solver Parameters
"smoother": "DADI",
"MGCycle": "sg",
"nSubiterTurb": 10,
"infchangecorrection": True,
# ANK Solver Parameters
"useANKSolver": True,
# NK Solver Parameters
"useNKSolver": True,
"nkswitchtol": 1e-6,
# Termination Criteria
"L2Convergence": 1e-10,
"L2ConvergenceCoarse": 1e-2,
"nCycles": 10000,
# Adjoint Parameters
"adjointL2Convergence": 1e-10,
"ADPC": True,
}
# Create solver
CFDSolver = ADFLOW(options=aeroOptions, comm=comm)
CFDSolver.addLiftDistribution(150, "z")
CFDSolver.addSlices("z", np.linspace(0.1, 14, 10))
The set-up for adflow should look the same as for the wing aerodynamic analysis script.
However, note that we have added a tolerance setting for the adjoint and the infchangecorrection to update the angle-of-attack throughout the flow field when the optimzier updates it.
Unlike the airfoil optimzation example, these settings are not tuned for this particular wing optimziation problem.
We add a single lift distribution with 150 sampling points.
Set the AeroProblem
ap = AeroProblem(name="wing", alpha=1.5, mach=0.8, altitude=10000, areaRef=45.5, chordRef=3.25, evalFuncs=["cl", "cd"])
# Add angle of attack variable
ap.addDV("alpha", value=1.5, lower=0, upper=10.0, scale=0.1)
The only difference in setting up the AeroProblem is that now we add angle-of-attack as a design variable. Any of the quantities included in the initialization of the AeroProblem can be added as design variables.
Geometric parametrization
# Create DVGeometry object
FFDFile = "../ffd/ffd.xyz"
DVGeo = DVGeometry(FFDFile)
# Create reference axis
nRefAxPts = DVGeo.addRefAxis("wing", xFraction=0.25, alignIndex="k")
nTwist = nRefAxPts - 1
# Set up global design variables
def twist(val, geo):
for i in range(1, nRefAxPts):
geo.rot_z["wing"].coef[i] = val[i - 1]
DVGeo.addGlobalDV(dvName="twist", value=[0] * nTwist, func=twist, lower=-10, upper=10, scale=0.01)
# Set up local design variables
DVGeo.addLocalDV("local", lower=-0.5, upper=0.5, axis="y", scale=1)
# Add DVGeo object to CFD solver
CFDSolver.setDVGeo(DVGeo)
The set-up for DVGeometry should look very familiar (if not, see Geometric Parametrization).
We include twist and local variables in the optimization.
After setting up the DVGeometry instance we have to provide it to ADflow with the call setDVGeo.
Geometric constraints
We can set up constraints on the geometry with the DVConstraints class, also found in the pyGeo module. There are several built-in constraint functions within the DVConstraints class, including thickness, surface area, volume, location, and general linear constraints. The majority of the constraints are defined based on a triangulated-surface representation of the wing obtained from ADflow.
Note
The triangulated surface is created by ADflow (or DAfoam) using the wall surfaces defined in the CFD volume mesh. The resolution is similar to the CFD surface mesh, and users do not need to provide this triangulated mesh themselves.
Optionally, this can also be defined with an external file, see the docstrings for setSurface().
This is useful if users want to have a different resolution on the triangulated surface (finer or coarser) compared to the CFD mesh, or if DVConstraints is being used without ADflow (or DAfoam).
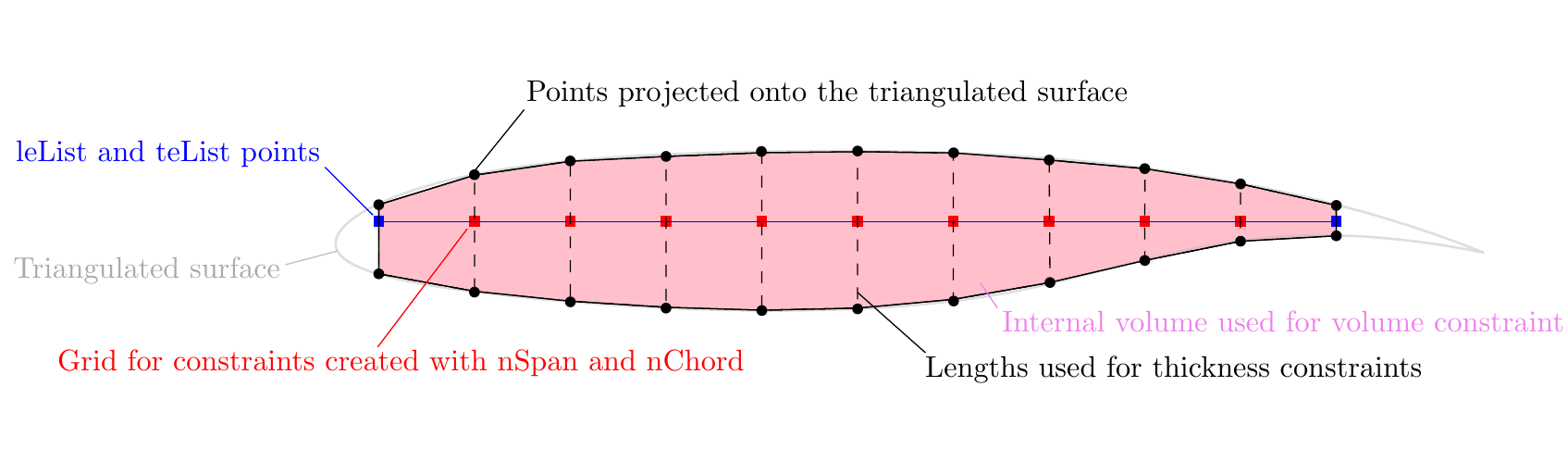
The volume and thickness constraints are set up by creating a uniformly spaced 2D grid of points, which is then projected onto the upper and lower surface of a triangulated-surface representation of the wing.
The grid is defined by providing four corner points (using leList and teList) and by specifying the number of spanwise and chordwise points (using nSpan and nChord).
Note
These grid points are projected onto the triangulated surface along the normals of the ruled surface formed by these grid points.
Typically, leList and teList are given such that the two curves lie in a plane.
This ensures that the projection vectors are always exactly normal to this plane.
If the surface formed by leList and teList is not planar, issues can arise near the end of an open surface (i.e., the root of a wing) which can result in failing intersections.
By default, scaled=True for addVolumeConstraint() and addThicknessConstraints2D(), which means that the volume and thicknesses calculated will be scaled by the initial values (i.e., they will be normalized).
Therefore, lower=1.0 in this example means that the lower limits for these constraints are the initial values (i.e., if lower=0.5 then the lower limits would be half the initial volume and thicknesses).
Warning
The leList and teList points must lie completely inside the wing.
DVCon = DVConstraints()
DVCon.setDVGeo(DVGeo)
# Only ADflow has the getTriangulatedSurface Function
DVCon.setSurface(CFDSolver.getTriangulatedMeshSurface())
# Volume constraints
leList = [[0.01, 0, 0.001], [7.51, 0, 13.99]]
teList = [[4.99, 0, 0.001], [8.99, 0, 13.99]]
DVCon.addVolumeConstraint(leList, teList, nSpan=20, nChord=20, lower=1.0, scaled=True)
# Thickness constraints
DVCon.addThicknessConstraints2D(leList, teList, nSpan=10, nChord=10, lower=1.0, scaled=True)
For the volume constraint, the volume is computed by adding up the volumes of the prisms that make up the projected grid as illustrated in the following image (only showing a section for clarity). For the thickness constraints, the distances between the upper and lower projected points are used, as illustrated in the following image. During optimization, these projected points are also moved by the FFD, just like the wing surface, and are used again to calculate the thicknesses and volume for the new designs. More information on the options can be found in the pyGeo docs or by looking at the pyGeo source code.
The LeTe constraints (short for Leading edge/Trailing edge constraints) are linear constraints based on the FFD control points.
When we have both twist and local shape variables, we want to prevent the local shape variables from creating a shearing twist.
This is done by constraining the upper and lower FFD control points on the leading and trailing edges to move in opposite directions.
Note that the LeTe constraint is not related to the leList and teList points discussed above.
# Le/Te constraints
DVCon.addLeTeConstraints(0, "iLow")
DVCon.addLeTeConstraints(0, "iHigh")
if comm.rank == 0:
# Only make one processor do this
DVCon.writeTecplot(os.path.join(args.output, "constraints.dat"))
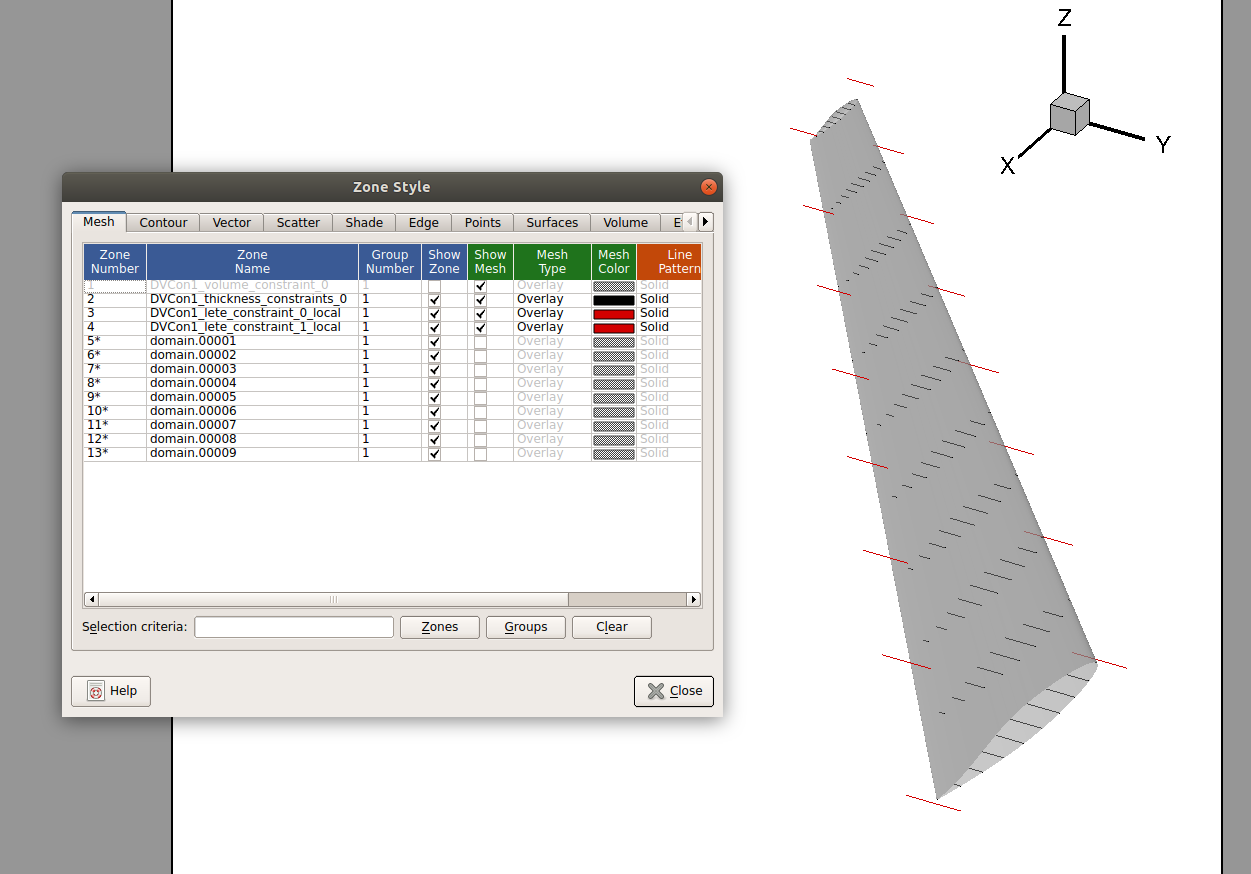
In this script DVCon.writeTecplot will save a file named constraints.dat which can be opened with Tecplot to visualize and check these constraints.
Since this is added here, before the commands that run the optimization, the file will correspond to the initial geometry.
The following image shows the constraints visualized with the wing surface superimposed.
This command can also be added at the end of the script to visualize the final constraints.
Mesh warping set-up
meshOptions = {"gridFile": args.gridFile}
mesh = USMesh(options=meshOptions, comm=comm)
CFDSolver.setMesh(mesh)
This is as straightforward as it was in the airfoil optimziation tutorial.
Optimization callback functions
def cruiseFuncs(x):
if comm.rank == 0:
print(x)
# Set design vars
DVGeo.setDesignVars(x)
ap.setDesignVars(x)
# Run CFD
CFDSolver(ap)
# Evaluate functions
funcs = {}
DVCon.evalFunctions(funcs)
CFDSolver.evalFunctions(ap, funcs)
CFDSolver.checkSolutionFailure(ap, funcs)
if comm.rank == 0:
print(funcs)
return funcs
def cruiseFuncsSens(x, funcs):
funcsSens = {}
DVCon.evalFunctionsSens(funcsSens)
CFDSolver.evalFunctionsSens(ap, funcsSens)
CFDSolver.checkAdjointFailure(ap, funcsSens)
return funcsSens
def objCon(funcs, printOK):
# Assemble the objective and any additional constraints:
funcs["obj"] = funcs[ap["cd"]]
funcs["cl_con_" + ap.name] = funcs[ap["cl"]] - 0.5
if printOK:
print("funcs in obj:", funcs)
return funcs
This section is identical to the one in the airfoil optimization tutorial.
Optimization problem
# Create optimization problem
optProb = Optimization("opt", MP.obj, comm=comm)
# Add objective
optProb.addObj("obj", scale=1e2)
# Add variables from the AeroProblem
ap.addVariablesPyOpt(optProb)
# Add DVGeo variables
DVGeo.addVariablesPyOpt(optProb)
# Add constraints
DVCon.addConstraintsPyOpt(optProb)
optProb.addCon("cl_con_" + ap.name, lower=0.0, scale=10.0)
# The MP object needs the 'obj' and 'sens' function for each proc set,
# the optimization problem and what the objcon function is:
MP.setProcSetObjFunc("cruise", cruiseFuncs)
MP.setProcSetSensFunc("cruise", cruiseFuncsSens)
MP.setObjCon(objCon)
MP.setOptProb(optProb)
optProb.printSparsity()
This section is identical to the one in the airfoil optimization tutorial.
Run optimization
To finish up, we choose the optimizer and then run the optimization.
# Set up optimizer
if args.opt == "SLSQP":
optOptions = {"IFILE": os.path.join(args.output, "SLSQP.out")}
elif args.opt == "SNOPT":
optOptions = {
"Major feasibility tolerance": 1e-4,
"Major optimality tolerance": 1e-4,
"Hessian full memory": None,
"Function precision": 1e-8,
"Nonderivative linesearch": None,
"Print file": os.path.join(args.output, "SNOPT_print.out"),
"Summary file": os.path.join(args.output, "SNOPT_summary.out"),
"Major iterations limit": 1000,
}
elif args.opt == "IPOPT":
optOptions = {
"limited_memory_max_history": 1000,
"print_level": 5,
"tol": 1e-6,
"acceptable_tol": 1e-5,
"max_iter": 300,
"start_with_resto": "yes",
}
optOptions.update(args.optOptions)
opt = OPT(args.opt, options=optOptions)
# Run Optimization
sol = opt(optProb, MP.sens, storeHistory=os.path.join(args.output, "opt.hst"))
if comm.rank == 0:
print(sol)
Note
The complete set of options for SNOPT can be found in the pyOptSparse documentation.
It is useful to remember that you can include major iterations information in the history file by providing the proper options.
It has been observed that the _print and _summary files occasionally fail to be updated, possibly due to unknown hardware issues on GreatLakes.
The problem is not common, but if you want to avoid losing this information, you might back it up in the history file.
This would allow you monitor the optimization even if the _print and _summary files are not being updated.
Note that the size of the history file will increase due to this additional data.
Run it yourself!
To run the script, use the mpirun and place the total number of processors after the -np argument
mpiexec -n 4 python aero_opt.py
You can follow the progress of the optimization using OptView, as explained in Optimization with pyOptSparse.
Terminal output
An important step of verifyting the optimization setup is to check the sparsity structure of the constraint Jacobian:
+-------------------------------------------------------------------------------+
| Sparsity structure of constraint Jacobian |
+-------------------------------------------------------------------------------+
alpha_wing (1) twist (7) local (96)
+---------------------------------------+
DVCon1_volume_constraint_0 (1) | | X | X |
-----------------------------------------
DVCon1_thickness_constraints_0 (100) | | X | X |
-----------------------------------------
DVCon1_lete_constraint_0_local(L) (8) | | | X |
-----------------------------------------
DVCon1_lete_constraint_1_local(L) (8) | | | X |
-----------------------------------------
cl_con_wing (1) | X | X | X |
+---------------------------------------+
Postprocessing the solution output
All output is found in the output directory.
The naming scheme of the files follows in general <name>_<iter>_<type>.<ext>, where the <name> is aeroproblem, <iter> is the function evaluation number, <type> is the solution type (surface, volume, lift, slices, ect.), and <ext> is the file extension.
The solution files (.dat, .cgns or .plt) can be viewed in the Tecplot.
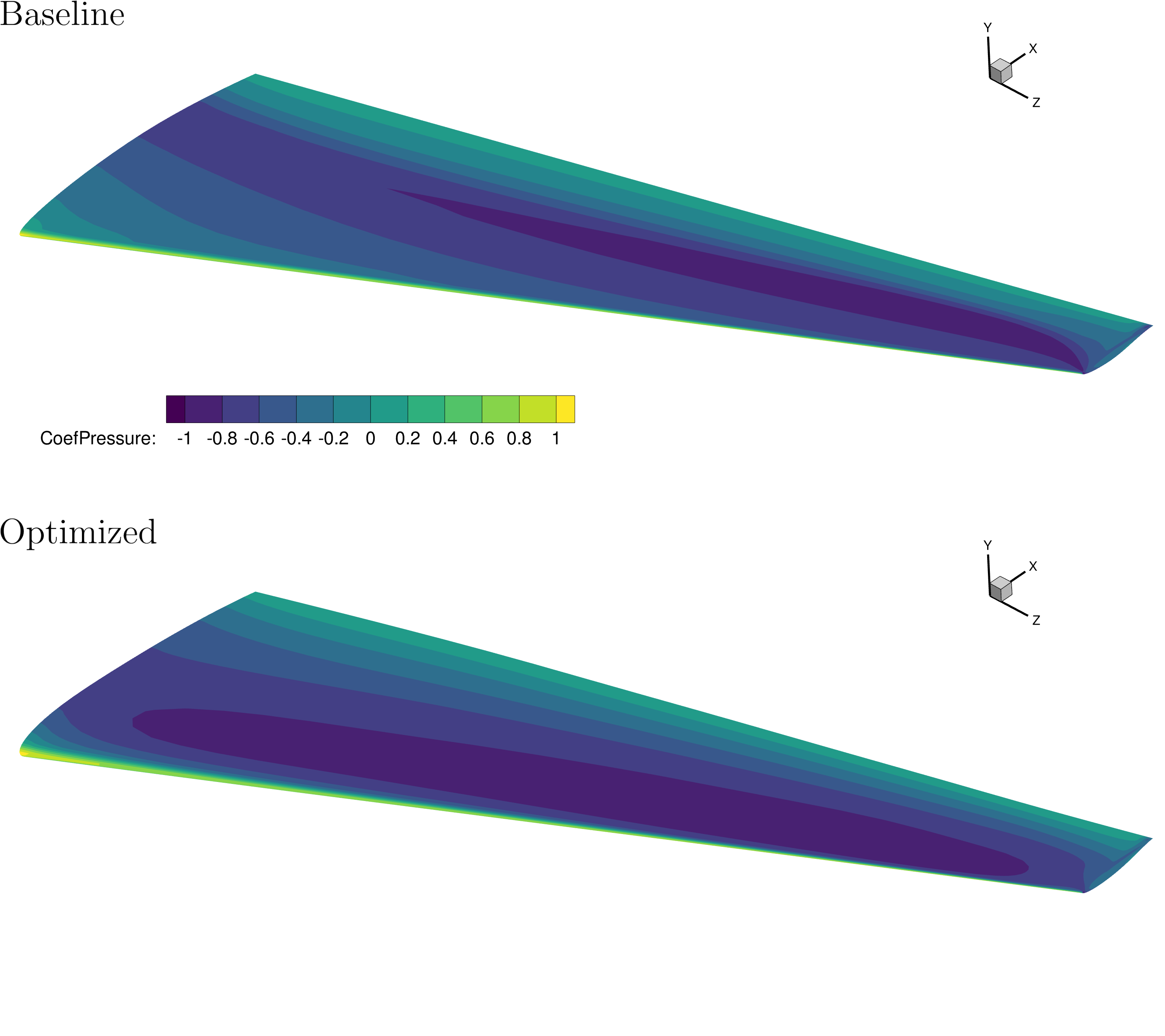
A contour plot of the pressure coefficient compared with the surface solution from the Analysis with ADflow is shown below.
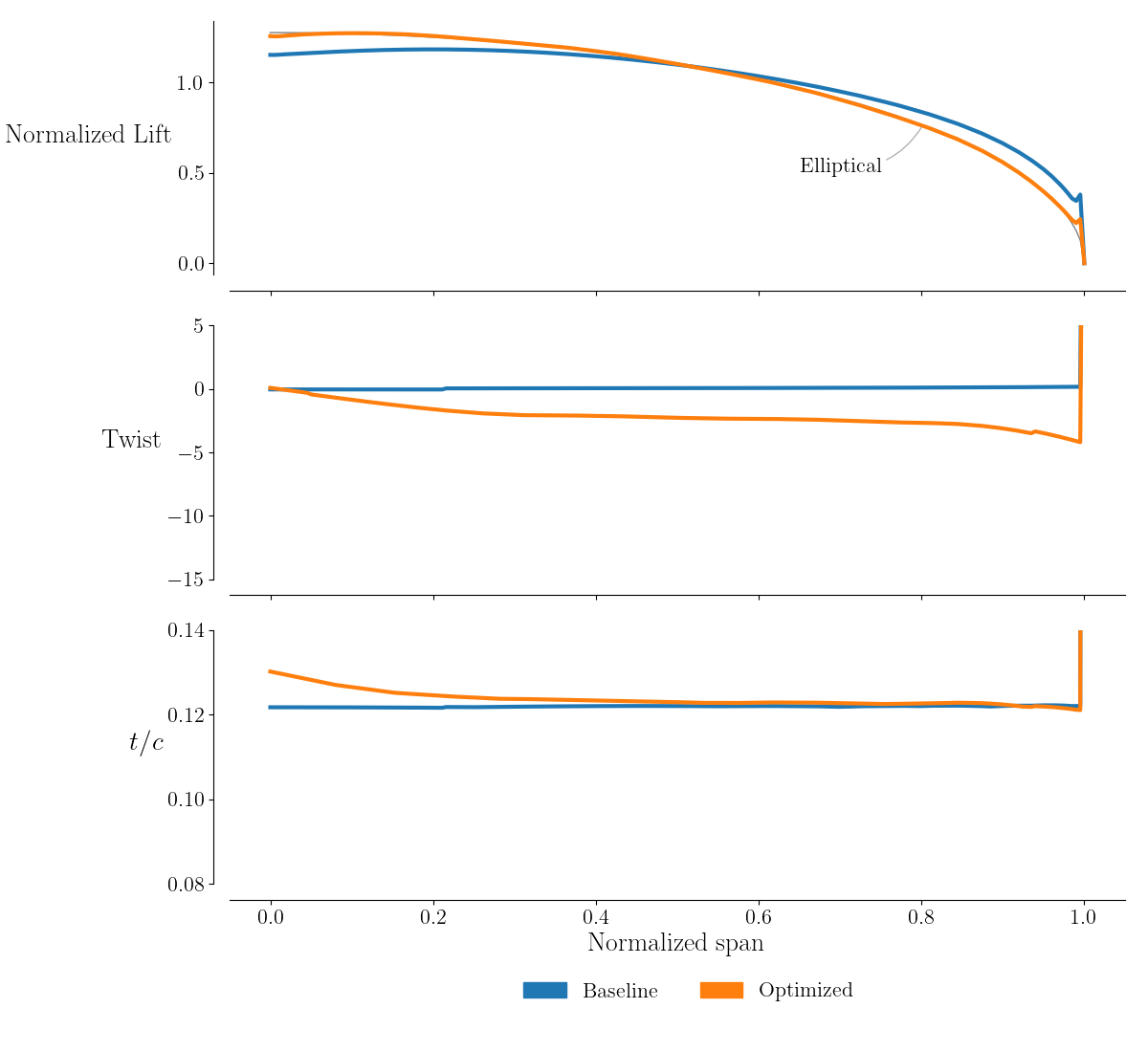
Similarly, as done in Analysis with ADflow, the lift and slice files (.dat) are used to compare the spanwise normalized lift, compared to elliptical lift, the twist distribution, and t/c.
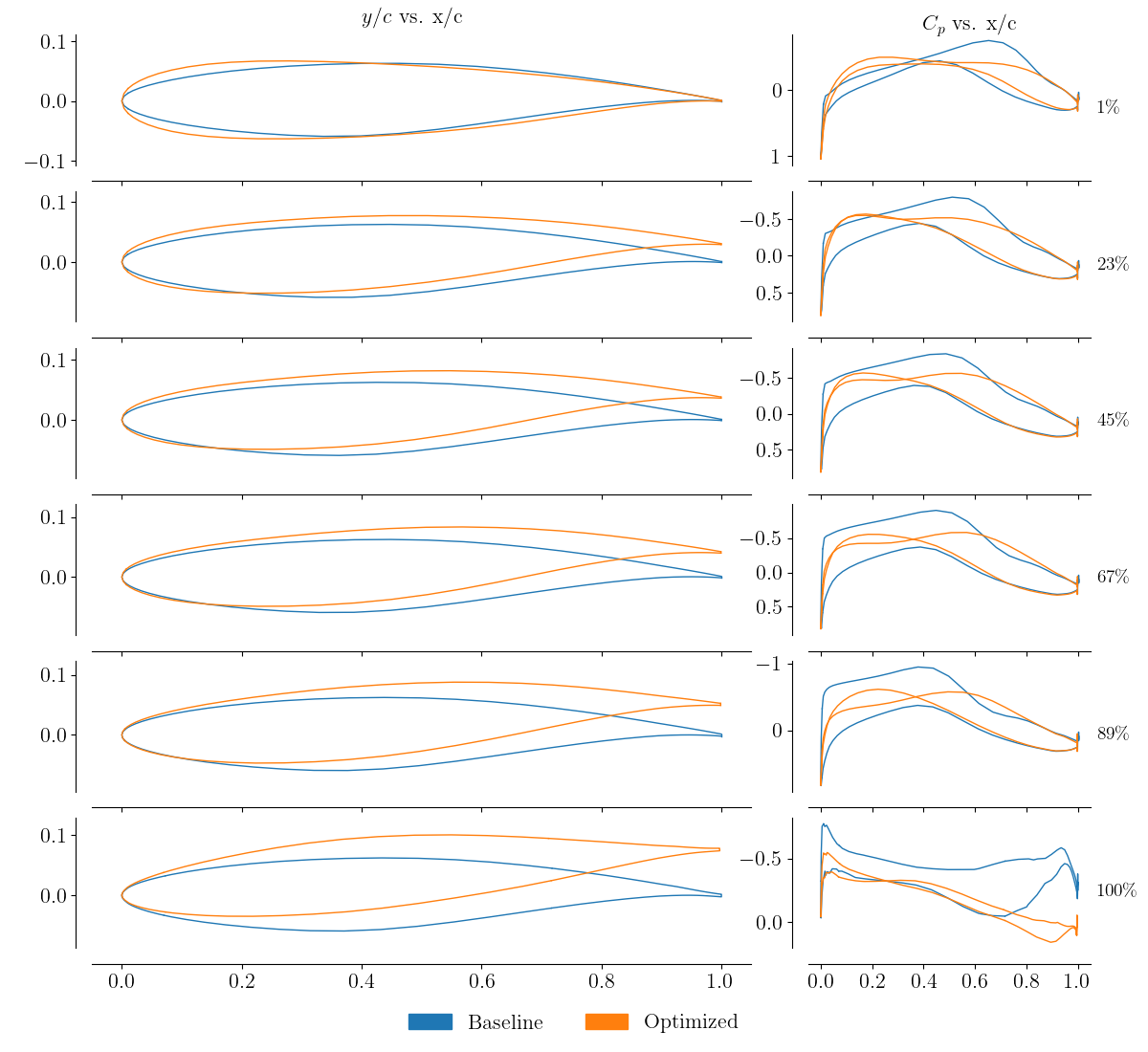
For the slice file, here the normalized airfoil shape and pressure coefficient are shown.
The optimized design achieves an elliptical lift distribution, and shows a more even and gradual pressure distribution as shown by the contour and section plots.
Further, the optimized twist distribution, as expected, demonstrates higher lift in the outboard section of the wing.
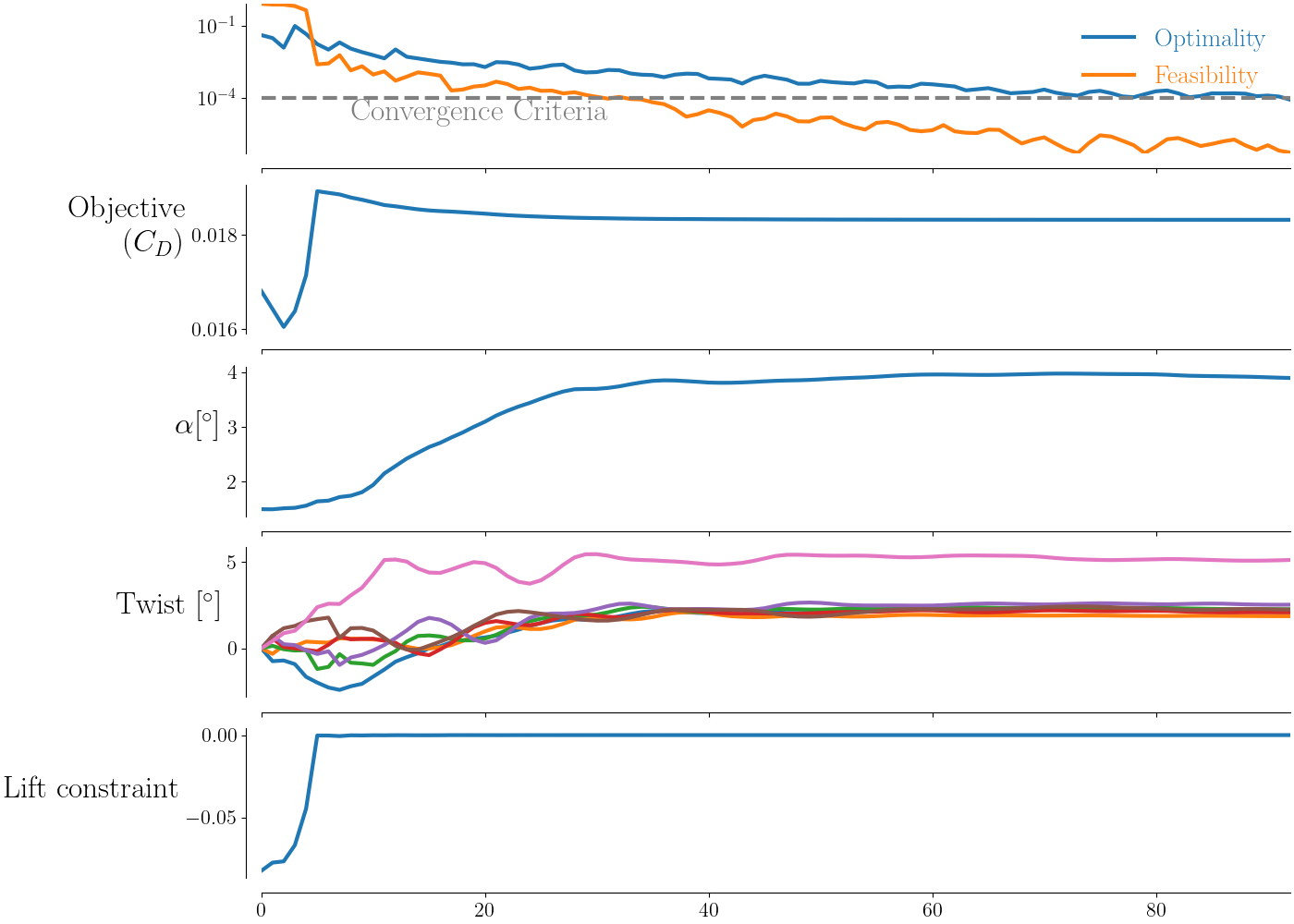
Finally the optimization history can be viewed either by parsing the database or using OptView. Here the former is done showing the major iterations of the history, objective, and some of the design variables and constraints. To produce the figure, run the accompanying postprocessing script as shown below.
python plot_optHist.py --histFile output/opt.hst --outputDir output/