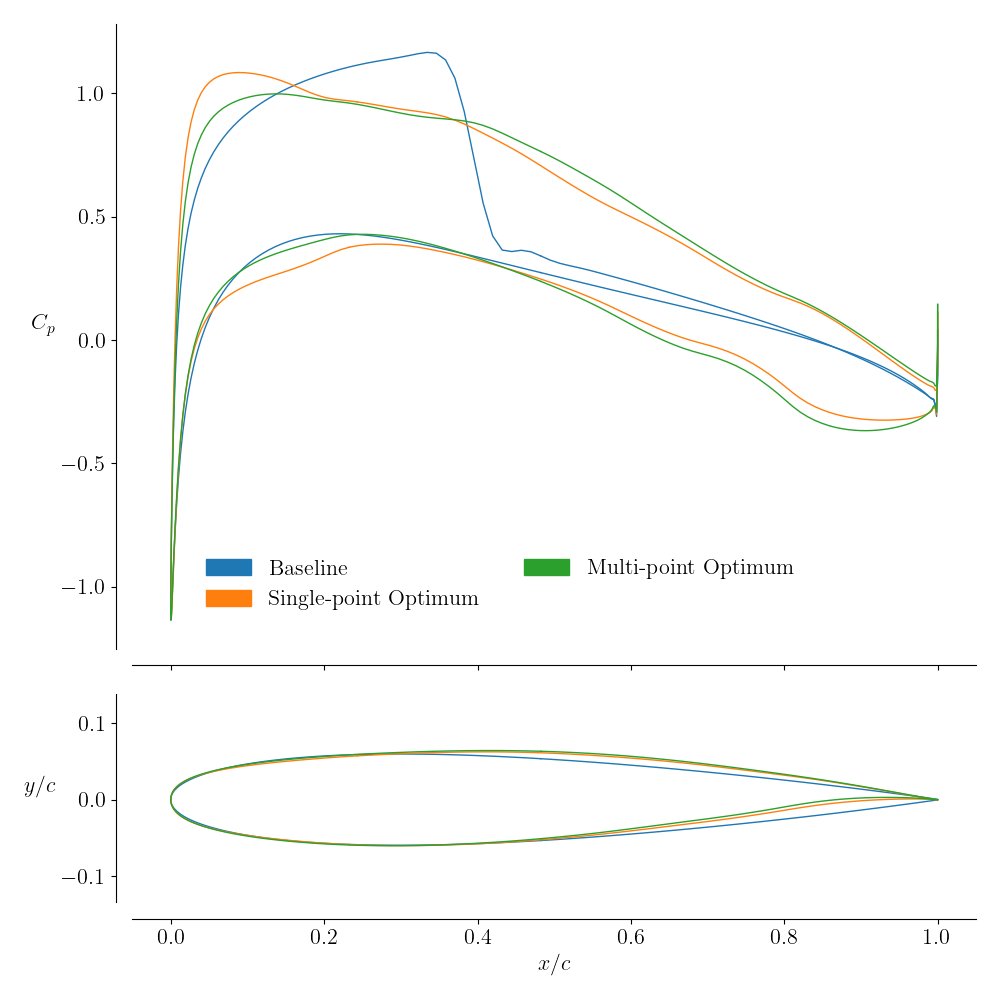
Multipoint Optimization

Introduction

Optimization does not have to be limited to a single flight condition. This section goes through the same optimization as the single point case, except with one more flight condition. Instead of rewriting the code from scratch, the differences in code will be pointed out.

Note

Different parallelizations are possible with multipoint optimizations. In this tutorial, all of the processors will be used to solve the first AeroProblem, then they will all switch and solve the second AeroProblem. Alternatively, it’s possible to solve both simultaneously by using twice the number of processors, but load balancing becomes an issue.

The optimization problem is defined as:

minimize

average drag: \(\frac{1}{2} \left(C_{D,0} + C_{D,1}\right)\)

with respect to

10 shape variables

subject to

\(C_{L,0} = 0.5\)
\(C_{L,1} = 0.7\)
\(V \ge V_0\)
\(t \ge 0.1t_0\)
\(\Delta z_\text{LETE, upper} = -\Delta z_{LETE, lower}\)

Files

Navigate to the directory airfoilopt/multipoint in your tutorial folder. Copy the singlepoint script from the previous section to a new file in this directory:

cp ../singlepoint/airfoil_opt.py airfoil_multiopt.py

Highlighting the changes required in the multipoint optimization script

Open the file airfoil_multiopt.py in your favorite text editor. Change the following sections for multipoint optimization.

Specifying parameters for the optimization

# specify flight conditions and constraints
mach = [0.75, 0.5]
alt = [10000, 5000]
alpha = [1.5, 5]
mycl = [0.5, 0.7]
# number of points in multipoint optimization
nFlowCases = len(mach)

For multipoint optimization, the parameters have to be specified in lists of the same size.

Creating processor sets

# assign number of processors
nGroup = 1
nProcPerGroup = MPI.COMM_WORLD.size
MP = multiPointSparse(MPI.COMM_WORLD)
MP.addProcessorSet("cruise", nMembers=nGroup, memberSizes=nProcPerGroup)
comm, setComm, setFlags, groupFlags, ptID = MP.createCommunicators()
if not os.path.exists(args.output):
    if comm.rank == 0:
        os.mkdir(args.output)

This is largely unchanged from the single-point case, since we use a very similar parallelization scheme. The only difference is in defining the variable nGroup which is used later on to distinguish between the two AeroProblems.

Set the AeroProblem

aeroProblems = []
for i in range(nFlowCases):
    ap = AeroProblem(
        name="fc%d" % i,
        alpha=alpha[i],
        mach=mach[i],
        altitude=alt[i],
        areaRef=1.0,
        chordRef=1.0,
        evalFuncs=["cl", "cd"],
    )
    # Add angle of attack variable
    ap.addDV("alpha", value=alpha[i], lower=0, upper=10.0, scale=1.0)
    aeroProblems.append(ap)

For more than one AeroProblem, a list needs to be created. Each AeroProblem is created with the respective optimization point and appended to the list.

Optimization callback functions

def cruiseFuncs(x):
    if MPI.COMM_WORLD.rank == 0:
        print(x)
    # Set design vars
    DVGeo.setDesignVars(x)
    # Evaluate functions
    funcs = {}
    DVCon.evalFunctions(funcs)

    for i in range(nFlowCases):
        if i % nGroup == ptID:
            aeroProblems[i].setDesignVars(x)
            CFDSolver(aeroProblems[i])
            CFDSolver.evalFunctions(aeroProblems[i], funcs)
            CFDSolver.checkSolutionFailure(aeroProblems[i], funcs)
    if MPI.COMM_WORLD.rank == 0:
        print(funcs)
    return funcs


def cruiseFuncsSens(x, funcs):
    funcsSens = {}
    DVCon.evalFunctionsSens(funcsSens)
    for i in range(nFlowCases):
        if i % nGroup == ptID:
            CFDSolver.evalFunctionsSens(aeroProblems[i], funcsSens)
            CFDSolver.checkAdjointFailure(aeroProblems[i], funcsSens)
    if MPI.COMM_WORLD.rank == 0:
        print(funcsSens)
    return funcsSens


def objCon(funcs, printOK):
    # Assemble the objective and any additional constraints:
    funcs["obj"] = 0.0
    for i in range(nFlowCases):
        ap = aeroProblems[i]
        funcs["obj"] += funcs[ap["cd"]] / nFlowCases
        funcs["cl_con_" + ap.name] = funcs[ap["cl"]] - mycl[i]
    if printOK:
        print("funcs in obj:", funcs)
    return funcs

The same for-loop needs to be added to the callback functions. The lines that require a call to the an AeroProblem is now put into a for-loop to iterate through all of them. In the objCon function, the \(c_l\) constraint is also placed into the for-loop.

Optimization problem

# Create optimization problem
optProb = Optimization("opt", MP.obj, comm=MPI.COMM_WORLD)

# Add objective
optProb.addObj("obj", scale=1e4)

# Add variables from the AeroProblem
for ap in aeroProblems:
    ap.addVariablesPyOpt(optProb)

# Add DVGeo variables
DVGeo.addVariablesPyOpt(optProb)

# Add constraints
DVCon.addConstraintsPyOpt(optProb)
for ap in aeroProblems:
    optProb.addCon(f"cl_con_{ap.name}", lower=0.0, upper=0.0, scale=1.0, wrt=[f"alpha_{ap.name}", "shape"])

# The MP object needs the 'obj' and 'sens' function for each proc set,
# the optimization problem and what the objcon function is:
MP.setProcSetObjFunc("cruise", cruiseFuncs)
MP.setProcSetSensFunc("cruise", cruiseFuncsSens)
MP.setObjCon(objCon)
MP.setOptProb(optProb)
optProb.printSparsity()

The only difference here is that we now have two different \(c_l\) constraints, one for each point. These are added in a loop. In addition, we use the wrt keyword to specify the variables that affect each lift constraint. In this case, the alpha from the other flight conditions do not impact the lift constraint, so they are set to zero.

Run it yourself!

The script can be run in the same way

mpiexec -n 4 python airfoil_multiopt.py | tee output.txt